Ασκήσεις/ ερωτήσεις επανάληψης - Μαθηματικά Β΄ Γυμνασίου - Σχ. Έτος 2013-14
- Πληροφοριακά Στοιχεία
- Κατηγορία: Μαθηματικά
- Δημοσιεύθηκε : Τετάρτη, 23 Μάρτιος 2016 20:32
- Εμφανίσεις: 2633
ΕΡΩΤΗΣΕΙΣ ΣΤΗΝ ΑΛΓΕΒΡΑ
Εξισώσεις
1. α)Τι ονομάζεται αριθμητική και αλγεβρική παράσταση;
β)Τι ονομάζουμε αναγωγή ομοίων όρων σε μια αλγεβρική παράσταση ;
γ) Να διατυπώσετε τις ιδιότητες των ισοτήτων.
2. Τι λέγεται εξίσωση και τι λύση ή ρίζα μιας εξίσωσης;
3.Να συμπληρώσετε τα κενά:
-
Αδύνατη εξίσωση λέγεται η εξίσωση που ……………………….
-
Ταυτότητα ή αόριστη εξίσωση λέγεται η εξίσωση που έχει ………………………..
-
Mπορούμε να μεταφέρουμε όρους από το ένα μέλος μιας εξίσωσης στο άλλο με ………………………………………...
3.Δίνονται παρακάτω οι διάφορες εργασίες που κάνουμε για να λύσουμε μία εξίσωση πρώτου βαθμού:
Χωρισμός γνωστών όρων από αγνώστους.
Απαλοιφή παρονομαστών.
Διαίρεση με το συντελεστή του αγνώστου.
Αναγωγή ομοίων όρων.
Απαλοιφή παρενθέσεων(εκτέλεση πράξεων)
Γράψτε δεξιά μπροστά από κάθε εργασία τον αριθμό ,που δείχνει την προτεραιότητά της(δηλαδή το 1 στην πρώτη εργασία που κάνουμε ,το 2 στη δεύτερη...,κ.λ.π.
Ανισώσεις
1)Να διατυπώσετε τις ιδιότητες των ανισοτήτων.
2.Να συμπληρώσετε τα κενά:
α)Λύσεις της ανίσωσης λέγονται οι τιμές της μεταβλητής για τις οποίες προκύπτουν ……………….… ανισότητες και το σύνολό τους λέγεται σύνολο λύσεων της ανίσωσης.
Οι λύσεις μιας ανίσωσης είναι γενικά ………………… και μπορούμε να τις παραστήσουμε πάνω …………...
β)Δύο ανισώσεις που αληθεύουν συγχρόνως για κάποιες τιμές της μεταβλητής λέγονται ……………………………...
Για να βρούμε τις κοινές λύσεις δύο ή περισσοτέρων ανισώσεων ,λύνουμε ………………. την καθεμία ανίσωση και στο τέλος παριστάνουμε τις λύσεις τους πάνω ……………………………
Τετραγωνική ρίζα
1.α)Τι λέγεται τετραγωνική ρίζα ενός θετικού αριθμού α και πως συμβολίζεται;
β)Η τετραγωνική ρίζα ενός θετικού αριθμού μπορεί να είναι αρνητικός αριθμός;
γ) Ένας αρνητικός αριθμός έχει τετραγωνική ρίζα;
2.Να συμπληρώσετε τα κενά:
α)= …………… β)=……………… γ)Αν τότε =………………………
3.α)Ποιοι αριθμοί ονομάζονται άρρητοι;
β)Το σύνολο που αποτελείται από τους ……………………και τους ………………….λέγεται
σύνολο των ……………………………… ………………………. και συμβολίζεται με ………
Η έννοια της συνάρτησης-Γραφική παράσταση συνάρτησης
1.α)Τι λέγεται συνάρτηση;
β)Τι λέγεται πίνακας τιμών μιας συνάρτησης ;
2.Τι λέγεται γραφική παράσταση μιας συνάρτησης;
Οι συναρτήσεις y=αx , y=αx+β
1. Να συμπληρώσετε τα κενά:
-
Αν δύο ποσά είναι ανάλογα ,τότε ο ………………….. των τιμών του ενός προς τις αντίστοιχες τιμές του άλλου είναι σταθερός.
-
Αν δύο ποσά είναι ανάλογα τότε οι τιμές y του ενός ποσού εκφράζονται ως συνάρτηση των τιμών του x του άλλου με την ισότητα ………………...
2.α)Ποια είναι η γραφική παράσταση της συνάρτησης y=αx;. Τι ονομάζεται κλίση της ευθείας ;
β)Ποια είναι η γραφική παράσταση της συνάρτησης y=αx+β, β≠0;
3. Να συμπληρώσετε τα κενά:
Ο άξονας x΄x έχει εξίσωση …………... Ο άξονας y΄y έχει εξίσωση …………...
Η συνάρτηση , x≠0
1.Να συμπληρώσετε τα κενά:
-
Αν δύο ποσά είναι αντιστρόφως ανάλογα ,τότε το ………………….. των αντίστοιχων τιμών του ενός προς τις αντίστοιχες τιμές του άλλου είναι σταθερό.
-
Αν δύο ποσά είναι αντιστρόφως ανάλογα τότε οι τιμές y του ενός ποσού εκφράζονται ως συνάρτηση των τιμών του x του άλλου με την ισότητα ………………...………………
2.Τι γνωρίζετε για τη γραφική παράσταση της συνάρτησης ,με x≠0 ;
ΕΡΩΤΗΣΕΙΣ ΣΤΗ ΓΕΩΜΕΤΡΙΑ
Εμβαδά
1.α)Από τι εξαρτάται το εμβαδόν μιας επίπεδης επιφάνειας;
β)Ποιες είναι οι μονάδες μέτρησης εμβαδού και ποια είναι η σχέση που τις συνδέει;
2.Με τι ισούται το εμβαδόν τετραγώνου ,ορθογωνίου , παραλληλογράμμου , τριγώνου , ορθογωνίου τριγώνου και τραπεζίου;
Πυθαγόρειο Θεώρημα
1. Διατυπώστε το Πυθαγόρειο Θεώρημα.
2. Διατυπώστε το αντίστροφο του Πυθαγορείου Θεωρήματος.
Τριγωνομετρικοί αριθμοί
1.Τι ονομάζεται ημίτονο ,συνημίτονο και εφαπτομένη μιας οξείας γωνίας ορθογωνίου τριγώνου ;
2.Με τι ισούται η κλίση α της ευθείας με εξίσωση y=αx;
3.Για οποιαδήποτε οξέια γωνία ω ισχύει: α) …<ημω<… β)…<συνω<…
4.Πως υπολογίζουμε τους τριγωνομετρικούς αριθμούς των 30ο ,45ο και 60ο ;
Εγγεγραμμένες γωνίες
1.α)Tι λέγεται εγγεγραμμένη γωνία σε έναν κύκλο;
β)Ποια είναι η σχέση της εγγεγραμμένης γωνίας με την επίκεντρη που έχει ίσο αντίστοιχο
τόξο;
2. Να συμπληρώσετε τα κενά:
-
Κάθε εγγεγραμμένη γωνία έχει μέτρο ίσο …………………………..του αντίστοιχου τόξου της .
-
Κάθε εγγεγραμμένη γωνία που βαίνει σε ημικύκλιο είναι ……………………
-
Οι εγγεγραμμένες γωνίες ενός κύκλου που βαίνουν στο ……………………... ή …………………. …………….. είναι ίσες.
Κανονικά πολύγωνα
1.Πότε ένα πολύγωνο λέγεται κανονικό;
2.α)Πως κατασκευάζουμε με τη βοήθεια ενός κύκλου κανονικό πολύγωνο με ν πλευρές;
β)Πότε ένας κύκλος λέγεται περιγγεγραμμένος σε πολύγωνο;
3. Να συμπληρώσετε τα κενά:
Σε ένα κανονικό ν-γωνο αν είναι ω η κεντρική του γωνία και φ μία από τις ίσες γωνίες του ,
ισχύει ότι: ω= …………………… και φ=…………...
Μήκος κύκλου -Εμβαδόν κυκλικού δίσκου
1.Να συμπληρώσετε τα κενά:
-
Αν L είναι το μήκος ενός κύκλου και η δ η διάμετρός του τότε =……..
-
Το εμβαδό Ε ενός κυκλικού δίσκου που έχει ακτίνα ρ είναι: Ε=………..
-
Αν διπλασιάσουμε την ακτίνα ενός κύκλου τότε το εμβαδό του αντίστοιχου κυκλικού δίσκου …………………………… ενώ το μήκος του ……………………
Επαναληπτικές ασκήσεις στην Άλγεβρα
1.Να λυθούν οι παρακάτω εξισώσεις:
α) 2 x -3 = x - 5 β) 9 x - 2 = 12 -1 - x γ) X + 4 = 2 + X δ) 3 Χ - 1 - 2Χ - 5 =5Χ + 1
2 4 5 5 3 4 6 12
2.Να βρεθεί ένας αριθμός ,του οποίου το διπλάσιο ,όταν αυξηθεί κατά 5 ,γίνεται ίσο με το τριπλάσιό του ελαττωμένο κατά 2.
3.Μία οικογένεια ξόδεψε τον προηγούμενο χρόνο το 1/2 των εσόδων της για ενοίκιο ,το 1/3 για φαγητό και άλλα έξοδα του σπιτιού , το 1/4 για ρούχα και το 1/12 για τα υπόλοιπα έξοδα. Ακόμα έκανε και αποταμίευση 200 ευρώ. Πόσα ήταν τα έσοδά της;
4.Να βρεθούν οι κοινές λύσεις των ανισώσεων :
α) 2(x-1 > 3(x-3) και 5x-2 > 2(x+5) β) Χ - 1 +Χ - 2 >Χ - 1 και 2 ( Χ - 1 ) < 3 ( Χ + 1)
2 3 4 3 4
5.Αν ο αριθμός α είναι η λύση της εξίσωσης
2 α - 4 + α = α - 1 + α - 1
2 3 5
να βρείτε τον αριθμό x για τον οποίο ισχύει:
x + 5 + 2 x + α + 1 - α = α x - 1 +4 x + 2 + 2x
α 2 5 2
6.Να βρεθεί αν η λύση της εξίσωσης
1 +3 x + 5 - x + 4 + 4 x + 1 = 2 x + 5
12 3 2 6 4
ανήκει στις λύσεις της παρακάτω ανίσωσης:
5 x - 4 > 4 x + 2
3 5
7.Ποιές από τις παρακάτω προτάσεις είναι σωστές και ποιες λάθος;
8.Να υπολογίσετε τις τιμές των παραστάσεων :
α)β)
9.Ένας οινοπαραγωγός έχει υπολογίσει ότι από κάθε κιλό σταφύλια παράγει 0,3 λίτρα κρασί.
α)Πόσα λίτρα κρασί θα πάρει από παραγωγή 800 κιλών σταφύλια;
β)Να εκφράσετε την ποσότητα σε λίτρα του κρασιού, που θα πάρει, ως συνάρτηση της ποσότητας των σταφυλιών που παράγει.
γ)Πόσα κιλά σταφύλια πρέπει να παράγει, ώστε να πάρει 120 λίτρα κρασί.
10. Δίνεται ο ακόλουθος πίνακας τιμών 2 ποσών. Να εξεταστεί αν τα ποσά είναι ανάλογα και να γραφτεί το y συναρτήσει του x.
|
x |
3 |
5 |
5,5 |
7 |
8,5 |
|
y |
0,6 |
1 |
1,1 |
1,4 |
1,7 |
11.Μία ευθεία διέρχεται από την αρχή των αξόνων και από το σημείο A(2,5).Να βρεθεί η συνάρτηση που έχει για γραφική παράσταση την ευθεία αυτή.
12.Η γραφική παράσταση της συνάρτησης y = λ ( 1 + x ) + 2 διέρχεται από το σημείο A (1, 4) .
α) Να υπολογιστεί το λ.
β) Να συμπληρωθεί ο ακόλουθος πίνακας:
|
x |
|
|
0 |
|
2 |
|
y |
-2 |
0 |
|
4 |
|
γ)Να γίνει η γραφική παράσταση, όταν . -2 ≤ x ≤ 2.
13.Δίνεται η συνάρτηση : y = α x + β
α)Να βρείτε τα α, β, αν είναι γνωστό ότι η ευθεία που την παριστάνει έχει κλίση 2 και ότι διέρχεται από το σημείο
( 0, -3).
β)Να σχεδιάσετε τη γραφική παράσταση της συνάρτησης.
14. Τα ποσά x και y είναι αντιστρόφως ανάλογα. Να συμπληρώσετε τον πίνακα με τις αντίστοιχες τιμές τους.
|
x |
60 |
12 |
|
30 |
|
y |
5 |
|
15 |
|
15.Δίνεται η συνάρτηση y = α / x.
Αν το σημείο ( 5, -1 ), είναι σημείο της γραφικής της παράστασης, να βρείτε τη συνάρτηση και να κάνετε τη γραφική της παράσταση.
Επαναληπτικές ασκήσεις στη Γεωμετρία
1.Σε ισοσκελές τρίγωνο ΑΒΓ είναι ΑΒ=ΑΓ=13cm και ΒΓ=10cm.
Nα υπολογίσετε το ύψος του ΑΚ.
2.Σε ορθογώνιο τρίγωνο ΑΒΓ είναι ΑΒ=15 cm και ΑΓ=20 cm.
α)Na υπολογίσετε την υποτείνουσα ΒΓ
β)Το εμβαδόν του τριγώνου
γ)Το ύψος ΑΔ που αντιστοιχεί στην υποτείνουσα
3.Σε ένα τρίγωνο ΑΒΓ φέρνουμε το ύψος ΑΔ. Αν ΑΒ=15 cm , ΑΔ=12 cm και ΑΓ=20 cm
α)Να υπολογίσετε το BΔ
β)Να υπολογίσετε το ΔΓ.
γ)Να εξετάσετε αν το τρίγωνο ΑΒΓ είναι ορθογώνιο
4.Δίνεται το ορθογώνιο τραπέζιο ΑΒΓΔ στο οποίο Α=Δ=90ο . Αν ΑΒ=4 cm ,ΒΓ=10 cm και ΓΔ=12 cm να υπολογίσετε
α)Το μήκος της πλευράς ΑΔ.
β)Το εμβαδόν του τριγώνου ΜΒΓ ,όπου Μ το μέσο της πλευράς ΑΔ.
5.Eνα τρίγωνο ΑΒΓ έχει ΒΓ=15 cm, ΑΓ=10 cm και Γ=30ο.
Nα βρείτε i)την πλευρά ΑΒ ii)το ύψος ΑΔ iii)το εμβαδό του.
6.Eνα τρίγωνο ΑΒΓ έχει Β=30ο ,Γ=45ο και ύψος ΑΔ=10 cm. Να βρεθούν οι πλευρές του ΒΔ, ΔΓ και το εμβαδό του. (Δίνεται )
7.Να υπολογιστεί το εμβαδόν του τραπεζίου
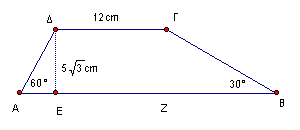
8.Στο διπλανό σχήμα είναι η γωνία ΒΑΔ=ω , εφω= 3/4 ,ΒΔ=9 cm και ΔΓ=16 cm.
α) Να υπολογίσετε το ύψος ΑΔ, τις πλευρές ΑΒ,ΑΓ.
β) Να δείξετε ότι το τρίγωνο ΑΒΓ είναι ορθογώνιο
γ) Να βρείτε το εμβαδόν του τριγώνου ΑΒΓ
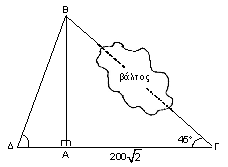
9.Ένας τοπογράφος θέλει να βρει την απόσταση μεταξύ των κτιρίων
Β και Γ στο ενδιάμεσο των οποίων παρεμβάλλεται ένας βάλτος.
Με τη βοήθεια ενός γεωμετρικού οργάνου προσδιόρισε ένα σημείο Α,
έτσι ώστε οι γωνίες ΒΑΓ = ΒΑΔ = 90?. Μετρώντας βρήκε τις αποστάσεις
ΑΓ = 200m και τη γωνία Γ = 45? (δες σχήμα).
Πόση είναι η απόσταση ΒΓ των κτιρίων;
0.Στο σχήμα 1 αν είναι το τόξο ΑΒΓ=150ο να βρείτε τις γωνίες ΑΔΓ και ΑΒΓ.
Σχήμα 1
11.Στο σχήμα 2 αν είναι το τόξο ΑΔ=40ο και το τόξο ΒΓ= 20Ο να βρεθεί η γωνία ΑΕΔ.
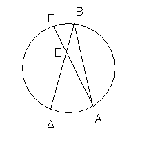 σχήμα 2
σχήμα 2
12. Σε κύκλο (Ο,ρ) παίρνουμε δύο διαδοχικές επίκεντρες γωνίες ΑKΒ=100ο και ΒKΓ=90ο .
Να υπολογισθούν οι γωνίες του τριγώνου ΑΒΓ.
13. Να συμπληρώσετε τον ακόλουθο πίνακα που αναφέρεται σε κανονικά πολύγωνα.
Πλήθος πλευρών |
Γωνία πολυγώνου |
Κεντρική γωνία |
|
3 |
|
|
|
|
150ο |
|
|
|
|
72ο
|
14.Σε ένα κύκλο με διάμετρο ΑΒ να φέρετε τις χορδές ΓΑ και ΓΒ.Αν είναι ΑΓ=9cm και ΒΓ=12cm να υπολογίσετε την περίμετρο του κύκλου.
15.Να βρείτε το μήκος του τόξου που αντιστοιχεί στην πλευρά τετραγώνου εγγεγραμμένου σε κύκλο με ακτίνα ρ=10cm.
16.Το εμβαδόν ενός κύκλου είναι 314 cm2.Να βρείτε το μήκος του.
17. Να υπολογίσετε το εμβαδό των γραμμοσκιασμένων επιφανειών (σχήμα 3 και σχήμα 4)
Σχήμα 3 Σχήμα 4
18.Στο διπλανό σχήμα η ακτίνα του κύκλου είναι 20 cm και η
ΑΒ=32 cm .Να βρεθεί το εμβαδό της γραμμοσκιασμένης επιφάνειας.
19.Σε έναν κύκλο με ακτίνα 12 cm να πάρετε ένα τόξο ΑΒ=90ο .
Να βρεθεί το εμβαδό του κυκλικού τμήματος που περικλείεται
από το τόξο ΑΒ και τη χορδή ΑΒ.
20.Στο ακόλουθο σχήμα οι διάμετροι ΑΒ, ΓΔ του κύκλου (Ο,ρ) τέμνονται κάθετα και τόξο .
α) Να υπολογίσετε τις γωνίες ,,
β) Αν το τόξο ΑΓ έχει μήκος 15,7 cm να υπολογίσετε το εμβαδόν του κυκλικού δίσκου (Ο,ρ).
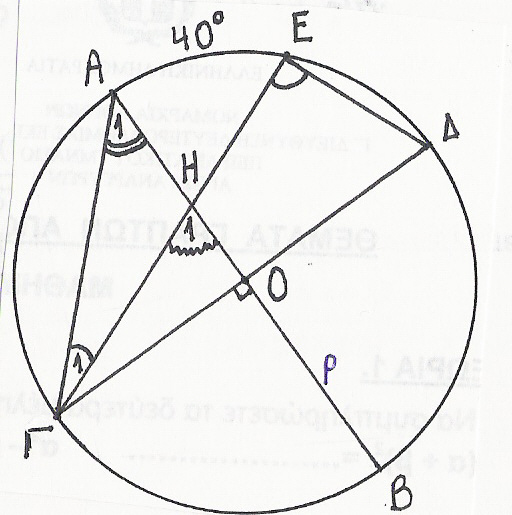
21.Στο ακόλουθο σχήμα, δίνεται ο κύκλος (Ο, ρ) με χορδή
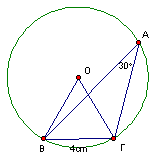
ΒΓ=4cm και γωνία . Να υπολογίσετε:
α) Την περίμετρο του τριγώνου ΟΒΓ
β) Το εμβαδόν του τριγώνου ΟΒΓ
γ) Το μήκος και το εμβαδόν του κύκλου